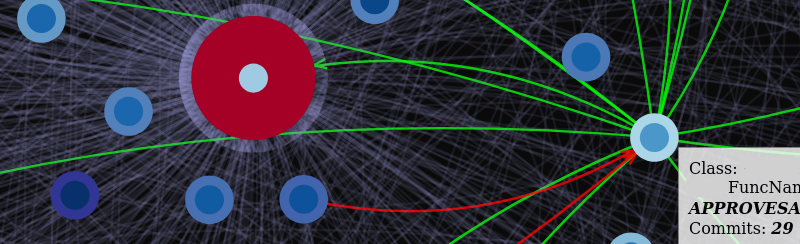
Have you ever spent hours on something, made it work, and then discovered a feature in the language that could have saved you a ton of effort? That’s what happened when I tried to figure out how to draw an arrowhead to a curved line at some distance from the center of a target (see banner).
TL;DR
When working with custom visualizations, you might need to do some math. But make use of (and give credit to) the community around these tools. It’s there for a reason.
Ready Aim Aim …
The title of this post refers to “the end”, and by that I mean “the end” of the curve from one point to another. But before we get there, let’s start from the beginning.
I was working on a custom visualization using D3.js 🔗 , and I decided to use a force-directed graph to help me spot cycles in a graph of calling and called Java classes. If you look at the diagram in the banner, each circle represents a class, and each arc represents a call from one class to another.
In more general terms, a diagram like this can represent just about any relationship between the circles, like a caller and the items it calls, or (an example for our times) somebody contagious and the people they have been in contact with. In graph theory 🔗 these are edges and nodes respectively. My goal was nothing more than a minor refinement of a well established visual representation of a directional graph with variable-sized nodes.
Rule number one when using D3: don’t re-invent the wheel. In building my new diagnostic tool I had started off the project with some examples [ 1 🔗 , 2 🔗 ] from the amazing D3 community, but I hadn’t found a force-directed graph with curved edges that used the faster Canvas rendering. The examples I had found were a huge help, but I still had to solve two problems:
- How to port the edge rendering logic from SVG to Canvas
- How to paint an arrowhead at an arbitrary distance from the center of the target node
I knew that before I drew the arrowhead I first needed to draw an arc through an aiming point some distance away from the line between two points in a two-dimensional plane. While D3 is amazing, and the community makes it even more powerful, there are times you need to dig into the math. Converting from SVG to Canvas meant a change in the path drawing code, and turning lines into curves called for an aiming point. But where exactly was that point?
My initial calculations made my head hurt (see my early notes below), and I nearly made it work, but this post isn’t about the value of keeping up math skills into your fifties (though one could make a case based on how tough the trig was), it’s about doing a different kind of homework: learning about your tools.
You see, while I had worked out a first formula to port the curve example to Canvas, I ran into a problem when the trajectory changed directions. In my initial calculation I aimed down and to the right, but I got some weird results from my Javascript functions when the direction changed.
A word of warning: before you find yourself transfixed by this problem (or worse, falling for my accidentally misleading use of Leibniz-like notation for simple division) don’t fall into the same rabbit hole I did. There’s a trick below that makes life very much easier than my first notes suspected. In short, I did need some math, but not quite as much as I thought.
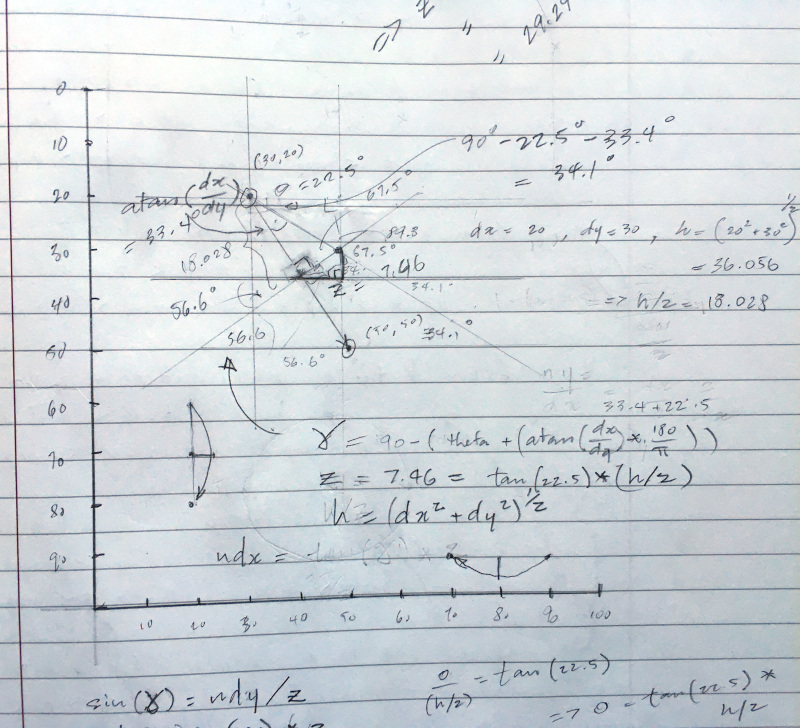
I had begun to worry I that the math changed depending on the direction, but the clock was ticking. I had already spent too long making the first few nodes work, and I needed to get back to the purpose of the visualization. Skipping straight to the punch line, you don’t need different math for every direction. You can just rotate the page!
Here is the function I wrote in Javascript to do the aiming:
function drawLink(d, i) {
context.beginPath();
context.lineWidth = 0.5;
context.strokeStyle = getLinkColour(d);
var dx = d.target.x - d.source.x,
dy = d.target.y - d.source.y,
hypot = Math.sqrt(dx * dx + dy * dy),
rotationAngle = Math.atan2(dy, dx),
controlPoint = {
x: Math.abs(hypot/2.0),
y: tan(DEFLECTION_ANGLE) * Math.abs(hypot/2.0)
};
/**
* Procedure:
* 1. translate to the starting point
* 2. rotate the drawing around the starting point placing the target east
* 3. aim to a control point floating 22.5 degrees above the midway point
* 4. draw an arrowhead (see below)
* 5. restore the original rotation and translation
*/
context.save();
context.translate(d.source.x, d.source.y);
context.rotate(rotationAngle);
context.moveTo(0, 0);
context.quadraticCurveTo(controlPoint.x, controlPoint.y, Math.abs(hypot), 0);
drawArrowhead(d, hypot, controlPoint);
context.restore();
context.stroke();
}
The comment block says it all: for each edge, go to the starting point of your arc and rotate the canvas so your target is due east! From there, calculating an aiming point is so much simpler.
Where it ends
The sample code is missing a part: drawing the arrowhead. You’ll notice in the banner of this post that my nodes are different sizes, so the position of the arrow’s tip had to move some distance back along the curve. The question was, how far? Again, my code comments contain the strategy.
function drawArrowhead(d, hypot, controlPoint) {
/**
* 1. calculate where the arrow hits the target's outer radius (contactPoint)
* 2. find the rotation angle from sin^-1(contactPoint.y/radius)
* 3. save, then rotate ccw
* 4. translate west length of radius
* 5. draw an arrowhead
* 6. restore
*/
var radius = outerCircleSize(d.target),
position = radius/hypot,
contactPoint = getQuadraticCurvePoint(0, 0, controlPoint.x,
controlPoint.y, hypot, 0, position)
tempRotation = Math.asin(contactPoint.y/radius);
context.save();
context.translate(hypot, 0); // go to target
context.rotate(-(tempRotation)); // flatten the curve
context.translate(-(radius), 0); // go to the arrow tip
context.moveTo(0.0, 0.0); // TODO: adjust for line thickness
context.lineTo(-2.5, -1.25); // draw one fin
context.moveTo(0.0, 0.0);
context.lineTo(-2.5, 0.75); // draw the other fin
context.restore();
}
But where did I get the contact point? That’s here, and credit for this goes to user AKX 🔗 at StackOverflow 🔗 :
function _getQBezierValue(t, p1, p2, p3) {
var iT = 1 - t;
return iT * iT * p1 + 2 * iT * t * p2 + t * t * p3;
}
function getQuadraticCurvePoint(startX, startY, cpX, cpY, endX, endY, position) {
return {
x: _getQBezierValue(position, startX, cpX, endX),
y: _getQBezierValue(position, startY, cpY, endY)
};
}
Conclusion
The Internet can be a wonderful place thanks to the generosity of people like Mike, Jody, and AKX whose solutions I relied on. In the spirit of paying it forward, I will be sharing my visualization in an upcoming post.